Leetcode 1653: Minimum Deletions to Make String Balanced

Leetcode • Jul 31, 2024

Recently I have been under a lot of stress at work, so I do LeetCode to relax. Unlike before, when I tried to learn new techniques, algorithms or data structures, this time I try to challenge myself to beat 100%. I have been successful several times this year. Let me share with you my thinking when trying to reach P100 for #1653: Minimum Deletions to Make String Balanced.

This is the Daily Challenge for 2024-07-30. The problem says:

You are given a string s consisting only of characters 'a' and 'b'​​​​. You can delete any number of characters in s to make s balanced. s is balanced if there is no pair of indices (i,j) such that i < j and s[i] = 'b' and s[j]= 'a'.

Return the minimum number of deletions needed to make s balanced.

As usual, Python is the language I prefer for solving LeetCode, not because it’s quite strangeforward, but also correct way to improve the runtime, the result will be reflected.

Analysis

We cannot apply greedy to this problem, i.e. counting a among b (or vice versa) and choosing the minimum cannot be the solution.

When looping from 0 -> n, we have to choose either to remove b or to keep it if we haven’t seen any b on the left. After choosing to keep the 1st b, we have to remove all the a in between. This is the atomic step of Dynamic Programming:

f(i) =
    if s[i] == 'b':
        f(i+1) if "has b on the left" else min(1 + f(i+1), f(i+1))
    else:
        f(i+1) + (1 if "has b on the left" else 0)

Solutions

1: Top-Down

First of all, let’s simulate the formula in a top-down manner

def minimumDeletions(self, s):
    @lru_cache(None)
    def dp(index, has_b):
        if index == len(s):
            return 0
        if s[index] == 'b':
            if has_b:
                return dp(index+1, True)
            else:
                return min(1+dp(index+1, False), dp(index + 1, True))
        else:
            return dp(index+1, has_b) + has_b
    return dp(0, False)

Note: In Python we don’t have to deal with memoir explicitly, Python has @lru_cache or @cache to help us store the map of inputs and outputs. Sometimes, it can cause OOM due to locating the DP inside a method, but it works most of the time.

The complexity is O(n) for both time and space. However, this got Memory Limit Exceeded on LeetCode. I’m not trying to solve this issue of top-down, but to move to a bottom-up approach.

2: Bottom-Up

def minimumDeletions(self, s):
    dp = [[0, 0] for _ in range(len(s) + 1)]
        
    for i in range(len(s)-1, -1, -1):
        if s[i] == 'b':
            dp[i][1] = dp[i+1][1]
            dp[i][0] = min(1+dp[i+1][0], dp[i+1][1])
        else:
            dp[i][1] = dp[i+1][1] + 1
            dp[i][0] = dp[i+1][0]
    return dp[0][0]

The same to before, but this time, we don’t need to use recursion, so, the memory won’t be eaten quickly due to the call-stack.

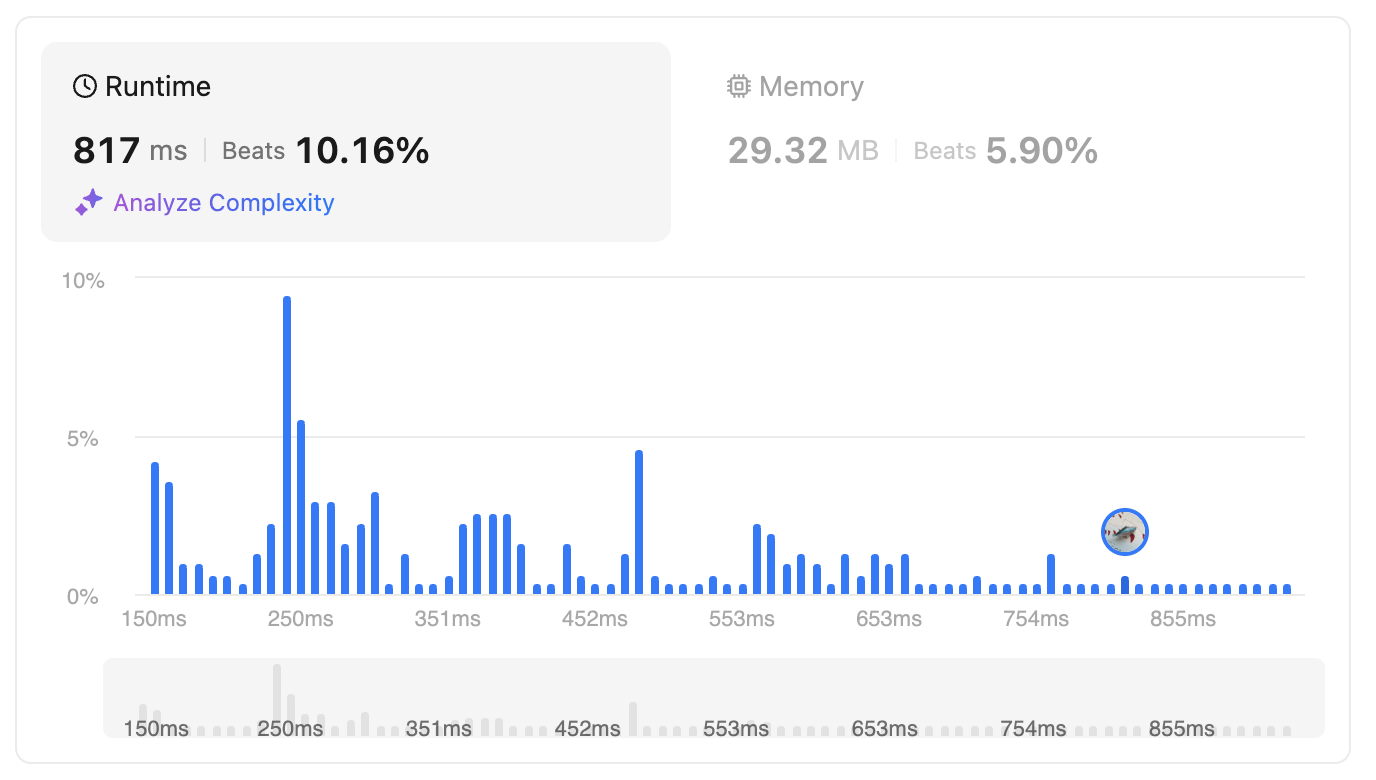
Same time and space complexity but we don’t get MLE anymore because of eliminating the recursion call-stack.

By the way, as we can see, it’s not required to store the whole table, at each step, only 2 states of the previous value are used. So, we can remove the dp.

Let’s move to #3

3.

def minimumDeletions(self, s: str) -> int:
    a, b = 0, 0
    for i in range(len(s)-1, -1, -1):
        if s[i] == 'b':
            a = min(1+a, b)
        else:
            b += 1
    return a

Here is what we got after reducing the memory usage to O(1)

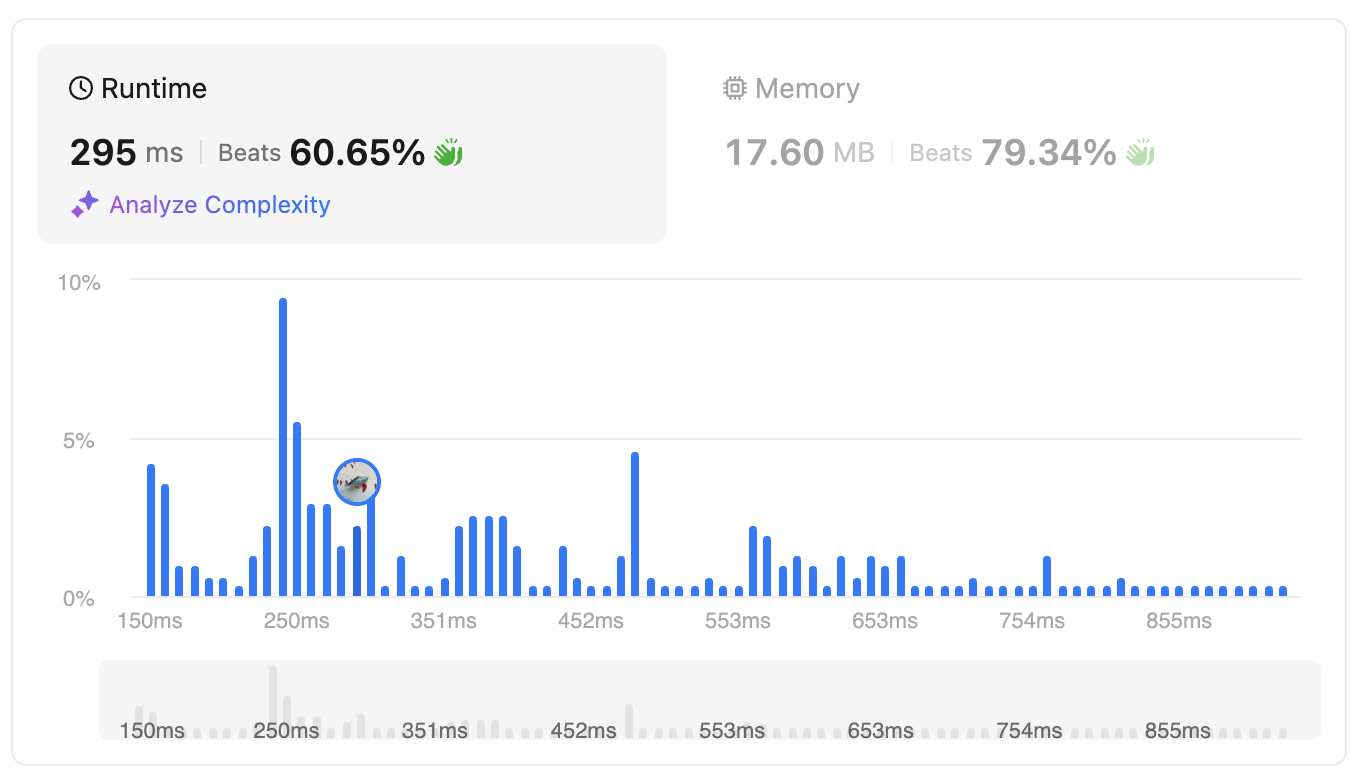
The result is much faster than #2, however, there are things we can do to improve the runtime.

4.

def minimumDeletions(self, s: str) -> int:
    a, b = 0, 0
    for i in range(len(s)-1, -1, -1):
        if s[i] == 'b':
            a = b if b < 1+a else 1+a
        else:
            b += 1
    return a

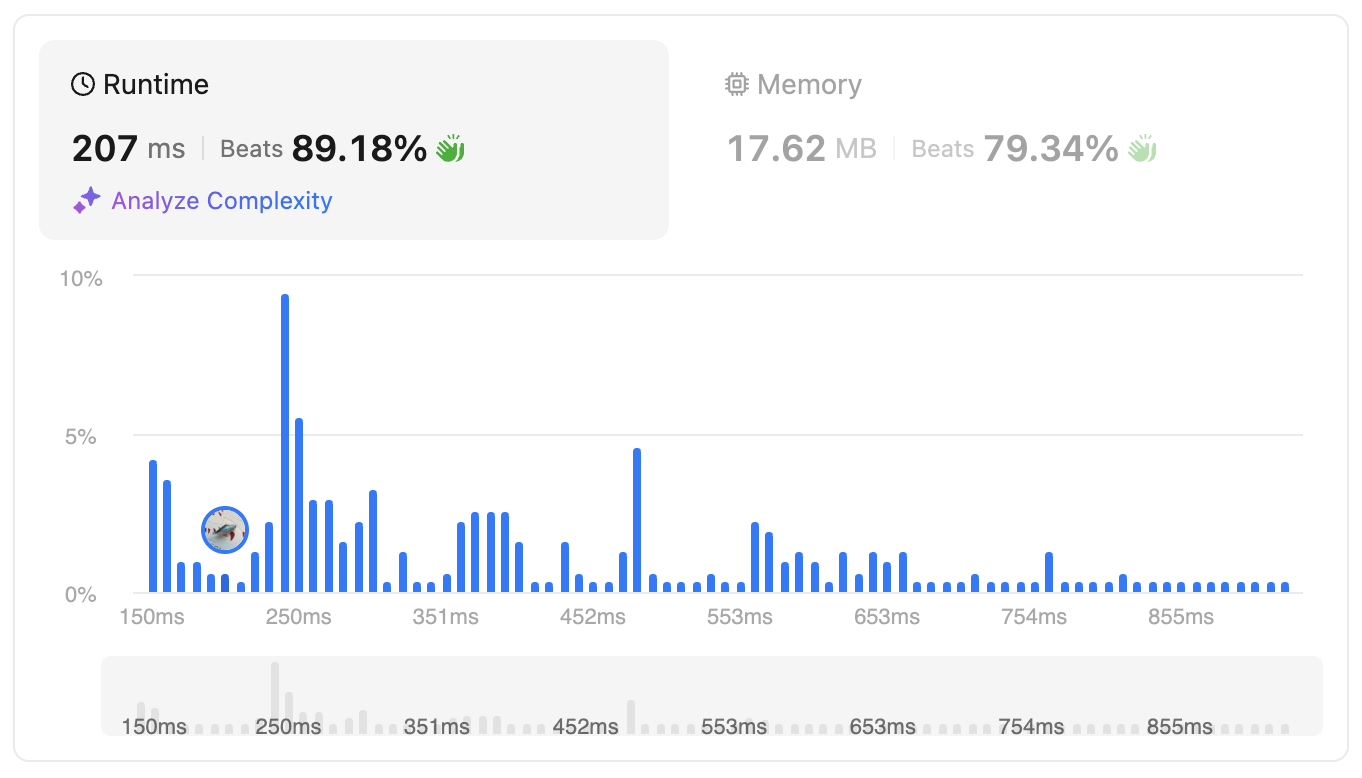
By eliminating the method call (min(1+a,b)), we also reduce the runtime by 90ms (~30% improvement). In the real product, if we could get a 30% performance improvement, that’s a big jump (unfortunately, in the real world, things are never that simple).

Of course, in the real production code, using min() is more intuitive than writing like a if a < b else b, and not using min() does not really have a big jump. (In Kotlin, we also have coerceAtLeast which is considered more readable in some cases).

5.

def minimumDeletions(self, s: str) -> int:
    a, b = 0, 0
    for c in s[::-1]:
        if c == 'b':
            a = b if b < 1+a else 1+a
        else:
            b += 1
    return a

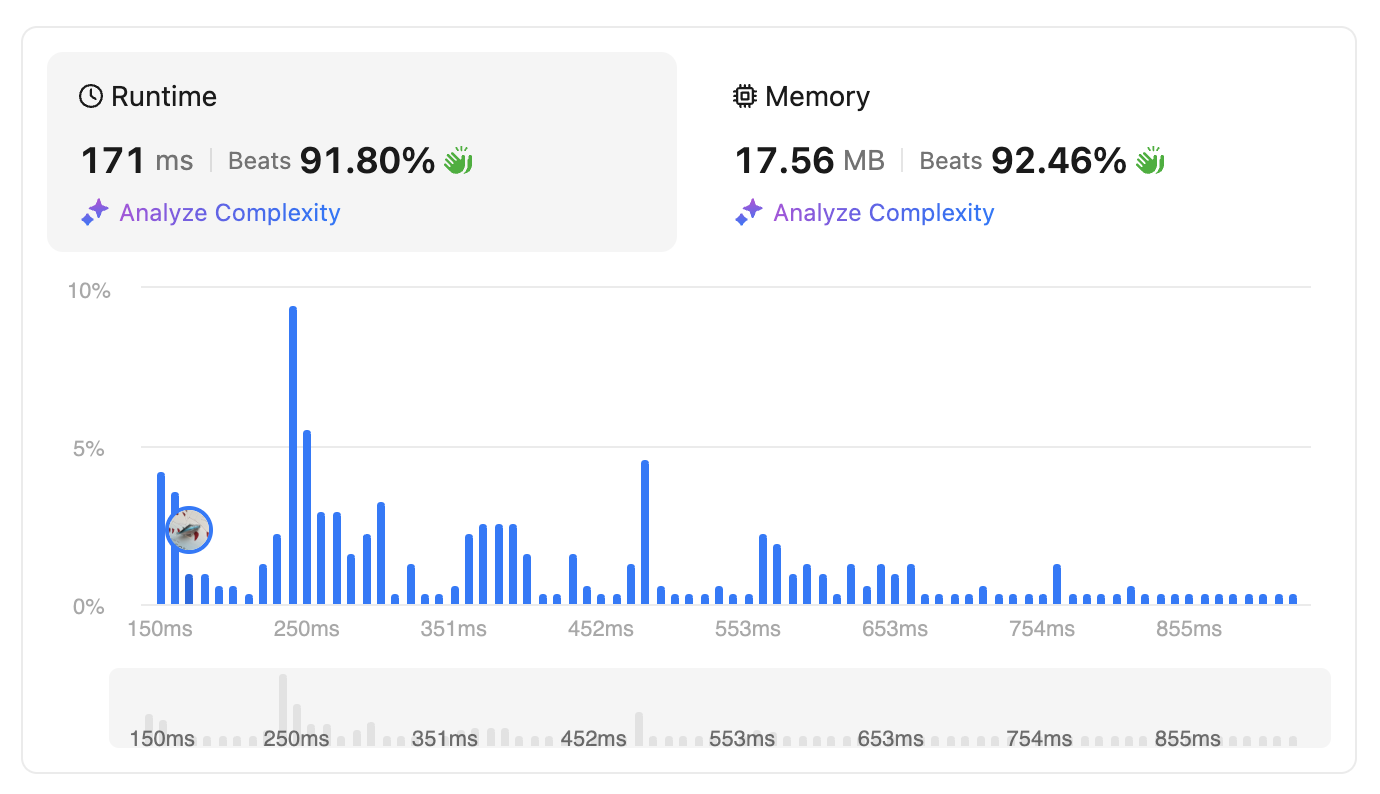
Since we don’t need the index anymore, we don’t need to use range'. Unlike the other language, Python does not have a char` datatype and also accessing an array or list takes some overhead. Therefore, using the language feature could improve performance. (because they are implemented in C/C++).

Is there any way we can improve? Of course there is! By the way, let’s reverse the order, instead of running from right to left, let’s run from left to right.

def minimumDeletions(self, s: str) -> int:
    a, b = 0, 0
    for c in s:
        if c == 'a':
            b = a if a < b+1 else 1+b
        else:
            a += 1
    return b

The result is unchanged (171ms), although we don’t see the inverted s anymore. Python does not actually create a new string when we reverse. I don’t dig deeper into Python’s implementation, so I don’t really know how it’s optimised, but we can guess that it’s similar to wrapping s[::-1] in a reverse(s) object and using it for iteration. This reduces a lot of memory usage.

Okay, now, let’s do some math.

6.

def minimumDeletions(self, s: str) -> int:
    a, b = 0, 0
    for c in s:
        if c == 'a':
            b = a if a <= b else 1+b
        else:
            a += 1
    return b

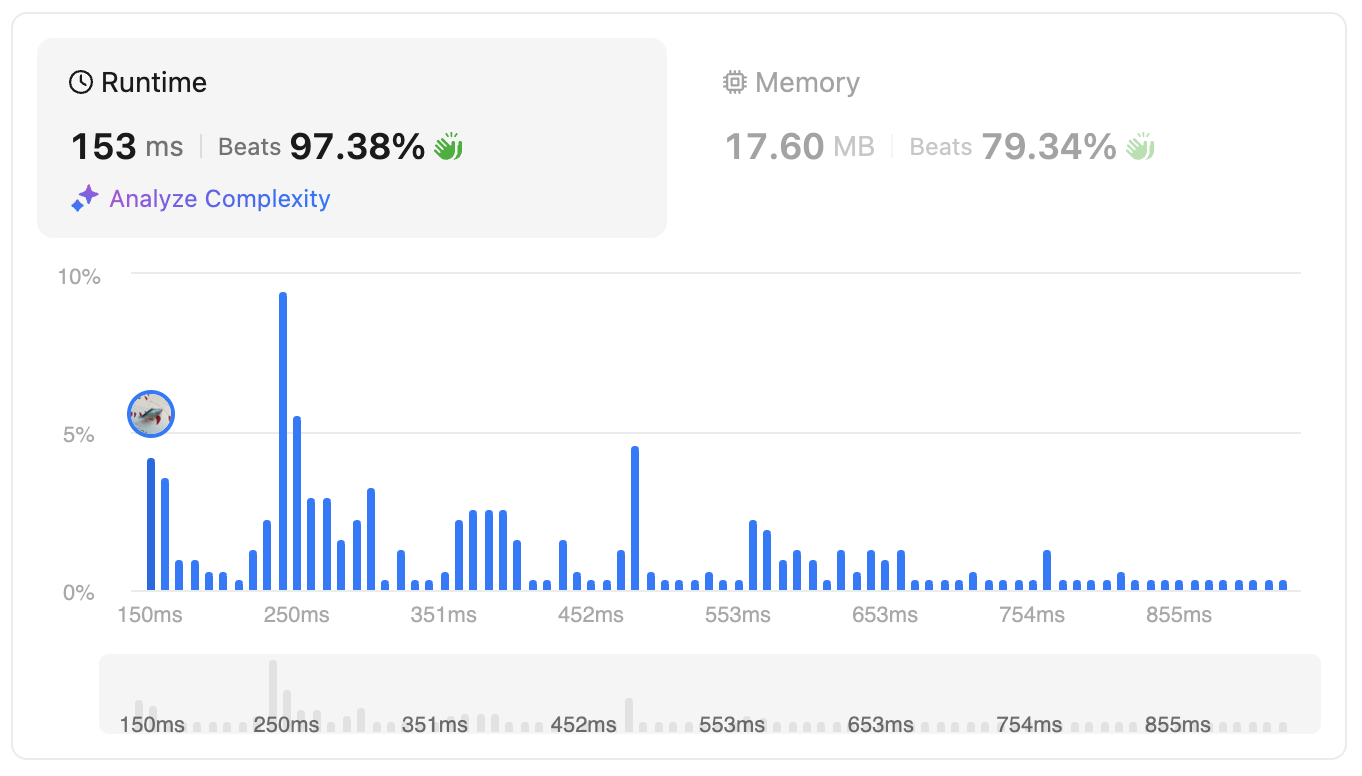
What happens? How can the code improve?

The answer is this line

b = a if a <= b else 1+b

In the previous version there are 2 1+b, which means we have to calculate twice. Any calculation takes time, and this is definitely true for Python. So by changing to an equivalent formula with less computation, we could improve the runtime by more than 10%.

Let’s do the math slowly

a < b+1

By removing +1, we can write a <= b for the boolean expression

There seems to be nothing else we can do now. We already change from looping i in range() to c in s, reduce the number of calculations by using a <= b instead of a < b+1.

And we still cannot beat 100%.

So, how?

7.

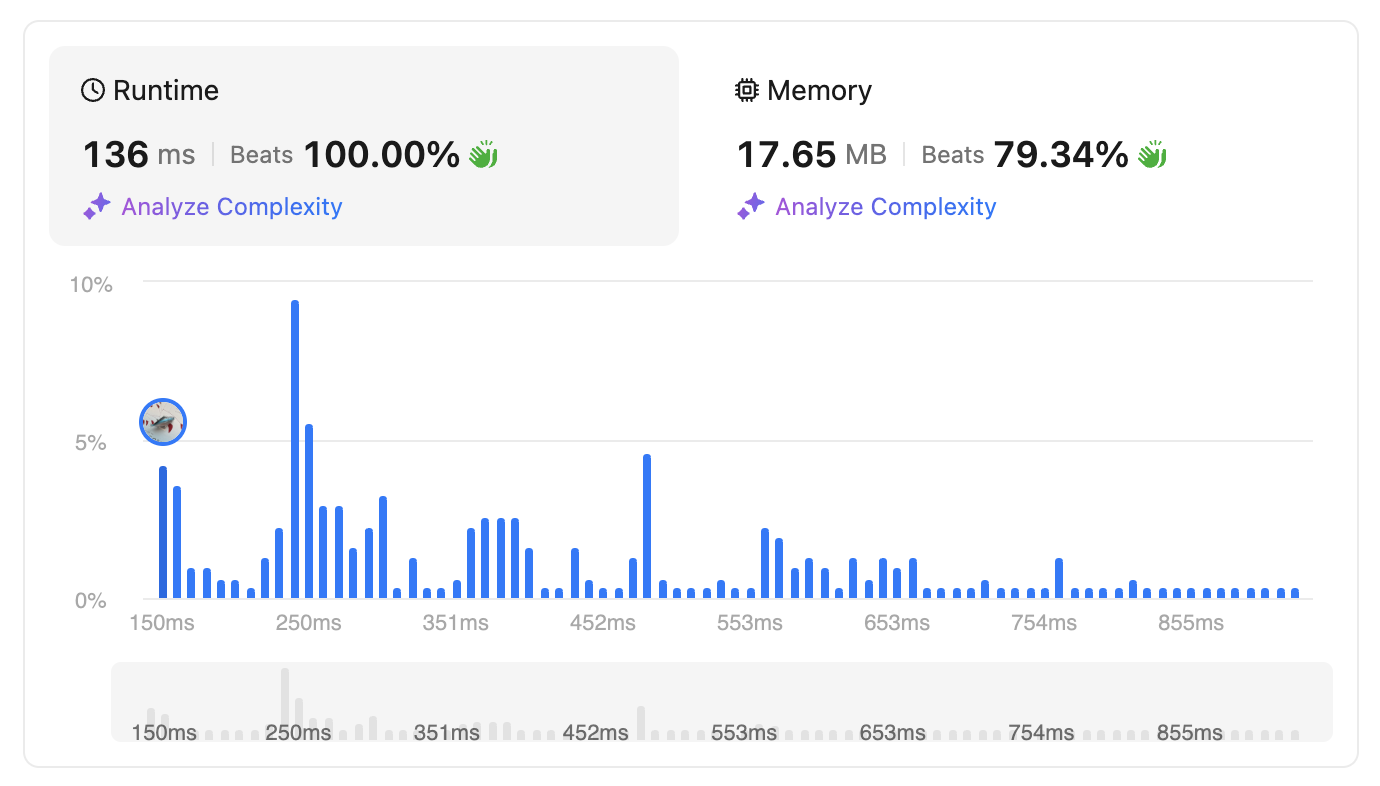
HOW?

def minimumDeletions(self, s: str) -> int:
    a, b = 0, 0
    for c in s:
        if c == 'a':
            b = 1+b if a > b else a
        else:
            a += 1
    return b

Err…? What happens? again.

I can say I got lucky for this result by submitting the code at the right time to get better result. So, the #7 is all about LUCK!

By the way, does changing a if a <= b else 1+b to 1+b if a > b else a really help? The answer is sighly maybe, but not in the way you thought.

Depending on the architecture, the answer lies under the assembly code of <= and > (or not).

In x86 assembly, there is no difference between <= and >, both need only 1 jump instruction (the same for ARM arch).

x86 Assembly >

cmp eax, ebx   ; Compare eax with ebx
jg greater     ; Jump to 'greater' if eax > ebx

x86 Assembly <=

cmp eax, ebx   ; Compare eax with ebx
jle less_equal ; Jump to 'less_equal' if eax <= ebx

However, with MIPS Assembly (which was used for the Computer Architecture subject in my University), it’s bit different

MIPS Assembly >

slt $t2, $t1, $t0  # $t2 = ($t1 < $t0) ? 1 : 0
bne $t2, $zero, greater  # if $t2 != 0, branch to 'greater'

MIPS Assembly <=

slt $t2, $t0, $t1  # $t2 = ($t0 < $t1) ? 1 : 0
beq $t2, $zero, equal_or_greater  # if $t2 == 0, branch to 'equal_or_greater'
ble $t0, $t1, less_equal  # if $t0 <= $t1, branch to 'less_equal'

As we can see, doing <= requires 2 commands in comparision to only 1 command when we do >. So, somehow, just by removing = from the comparision, we could improve the runtime by less than a nanosecond in MIPS.

Again, the result of #7 is just luck, the explanation above is just for fun or for someone whose curious mind on how the code works under the hood.

Conclusion

To beat 100%, all we need to do is click the Submit button several times and wish LeetCode will execute our code in the low traffic time.

Happy LeetCoding!